| Version 20 (modified by , 14 years ago) (diff) |
|---|
HadoopA51: Hadoop implementation of an rainbow table generator and searcher for cracking the A5/1 cypher
- Nume Scurt: HadoopA51
- SVN: https://svn-batch.grid.pub.ro/svn/PP2009/proiecte/HadoopA51/ (imported from the GIT repository)
- GIT: http://github.com/luciang/hadoop-rainbow-table-a51/ (with development history)
- Project members: Lucian Adrian Grijincu - lucian.grijincu
- Project description: the A5/1 cypher used to encrypt data sent over the air between a cell phone and a cell tower was proven broken several times. In 2009 a group of reserchers started to generate rainbow tables for A5/1 using CUDA machines. We seek to analise the generation of rainbow tables and the search on those tables on a distributed Hadoop cluster.
History & Motivation
History
A5/1 is one of the most prolific stream ciphers used worldwide (surpassing the one used in ssh or https by total size of encrypted data per year). It is used to provide OTA communication privacy and authentification in the GSM cell phone networks between a cell phone and the first cell tower.
Though at first the algorithm was not public, it was made available by researchers through reverse engineering and hardware monitoring. A reference implementation is given in https://svn-batch.grid.pub.ro/svn/PP2009/proiecte/HadoopA51/docs/a5/a5-1.c
Through time the algorithm was proven weak & broken (a selection of proofs):
- 1997 - Jovan Golic published "Cryptanalysis of Alleged A5 Stream Cipher" (http://jya.com/a5-hack.htm). Their attach uses a time-memory trade-off attack (based on the birthday paradox) which reveals an unknown internal state at a known time for a known keystream sequence. This internal state is then used to obtain the secret key.
- 2000 - Eli Biham and Orr Dunkelman analize A5/1 in "Cryptanalysis of the A5/1 GSM Stream Cipher" demonstrate an attack on A5/1 which relies on ~220 known plaintext data.
- 2003 - Barkan et al. published several active attacks on GSM by forcing a phone to use A5/2 (which is weaker than A5/1). As the key used in A5/2 and A5/1 in GSM implementations is the same, this lead to breaking the A5/1 code.
- 2005 - The same authors in "Conditional Estimators: An Effective Attack on A5/1" provide yet another attack on A5/1.
- 2009 - Karsten Nohl and Chris Paget provide details of an rainbow table attack on A5/1 in "GSM: SRSLY?" at the 26th Chaos Communication Congress (26C3). This attack was announched in September 2009 and lead to this project (HadoopA51)
Motivation
Such a wide used weak cypher must have sparked the interest of government agencies and criminal groups which want to gain illegal information shared through the cell phone.
Altough the cypher was proved broken several times before since at least 13 years ago, the GSM Association has not deployed another strong cypher to replace A5/1 (the proposed A5/3 is not yet supported in all networks or devices and it too was proven broken).
This project seeks to demonstrate that using commodity hardware organised in a Hadoop cluster can lead to an effective attack against A5/1.
Related Work
- http://cryptome.org/jya/a5-hack.htm - Cryptanalysis of Alleged A5 Stream Cipher
- https://svn-batch.grid.pub.ro/svn/PP2009/proiecte/HadoopA51/docs/a5/CS-2006-07.pdf - Instant Ciphertext-Only Cryptanalysis of GSM Encrypted Communication
- https://svn-batch.grid.pub.ro/svn/PP2009/proiecte/HadoopA51/docs/a5/a5-1.c - reference A5/1 implementation
- https://svn-batch.grid.pub.ro/svn/PP2009/proiecte/HadoopA51/docs/rainbow/Making%20a%20Faster%20Cryptanalytic%20Time-Memory%20Trade-Off%20-%20Oech03.pdf - A paper describing the rainbow table technique
- http://www.copacobana.org/paper/TC_COPACOBANA.pdf - Cryptanalysis with COPACOBANA
Project design
Rainbow tables
Table generation
Generating all possible outputs for known input strings of a certain length and all possible keys generates too much data making impractical storage and search of such an imense database.
To aleviate the shortcomings of this approach, we generate a number of precomputed hash chains organized as rainbow tables.
For each table, we define a set of reduction functions R that map hash values to secret values. The reduction functions used in each table must be different. This is needed because the R functions are not the inverses of H, the crypto function, so there are sets of input data that generate the same end values. This merger of two chains makes it difficult to determine which secret value generated a certain end secret. We solve this problem by generating a series of tables of chains. The probability of two mergers to happen at the same place and continue is smaller when we have different sets of reduction functions.
As it can be seen from the above image, the chain generation selects a set of random input values, applyes H (the crypto function, in our case A5/1) and then Ri. For each input secret value we only store the START and END secrets from the chain. Theoretically, chains can have any length we want (from 1-2 series of H and Ri applications to 215-220 applications). Practically smaller chains will lead to a need of bigger tables, while larger chains will increase the lookup time.
Table lookup
At lookup time, we need to find the secret that generated a hash value (encrypted secret) that we receive from the over-the-air communication between the cell phone and the nearest cell tower. Because we don't store all secret values in the rainbow tables, we need to run the Ri and H functions again until we find an end secret as in the following image:
Because more than one start secret value can lead to the same end secret, we need to filter only those start values that generate the secret on the i-th position from which we started the Ri and H chain leading to the current end secret.
Table generation
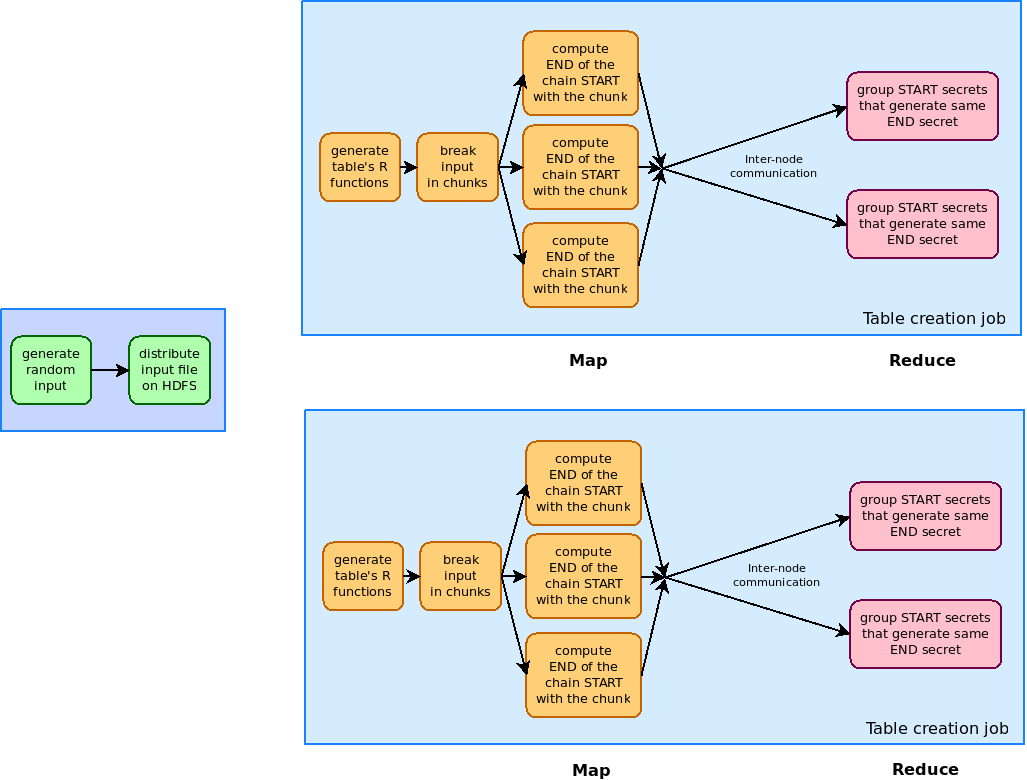
The table generation is split in two major phases:
- generating a set of random input data and distributing them in the Hadoop cluster over HDFS
- running multiple map-reduce jobs to compute the tables from the input data
The mapping phase of each map-reduce job reads one by one secrets from the distributed set of random secrets on the current Hadoop node and generates the chain of Ri and H applications. The result of a MAP instance is a <key, value> pair with the key being the end secret and the value being the start secret of that chain. We use this approach to skip a phase that otherwise would have been implemented manually: the end secrets need to be sorted and all their starting secrets gathered in the same place to simplify searching. This is implemented making use of the internal behaviour of Hadoop's MapReduce? implementation: the reducers receive a list of <key, value> pairs with the same key and reduce them to provide other <key, value> pairs. In our case the values are lists of starting secrets and the reducing part is just a merge of these lists.
The Map phase does little traffic outside the node (just receiving the set of random input secrets and the R function specifications). On the other hand, the Reducer phase does much traffic between nodes because it needs to gather all <key, value> pairs with the same key. By the nature of the A5/1 cypher and the R functions there is no simple corelation between the start secret and the end secret that can be used to reduce this inter-node communication.
In our tests we had only four Hadoop threads mapped on three machines (one dual core machine, and two single core ones). In such a limitted setup the amount of communication between the nodes was not a bottleneck, never reaching to saturate the available bandwidth (100Mbps). In real setups with tens-hundreds of Hadoop machines this may become a problem and may skewe out performance estimates.
Searching a hash
The last step of the attack is the search in the rainbow tables for the secret that might have generated a given hash value. This is again designed as a set of MapReduce? jobs that look in all tables for secrets generated by applying various numbers of Ri and H functions in order. Because Hadoop should take advantage of all cores on the machine it does not make sense to generate these end secrets on other threads. The Reduce part of the job combines the results and counts the number of aparition of each secret value. The final processing step must filter only those secrets that appear to have generated the hash value in all tables.
Performance
Our design would produce an estimated 64TiB of rainbow table data (if stored binary) and 64*240*[log_10_(medium_hash_value) + length of separators] (the last value is ~20) if stored as text files.
Attachments (4)
- map-reduce-table-generation.png (68.1 KB) - added by 14 years ago.
- rainbow.svg (53.3 KB) - added by 14 years ago.
- r-lookup.svg (32.9 KB) - added by 14 years ago.
- hadoop-rainbow-hashes.pdf (252.8 KB) - added by 14 years ago.
Download all attachments as: .zip
![(please configure the [header_logo] section in trac.ini)](/trac/PP2009/chrome/site/your_project_logo.png)