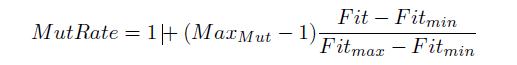| Version 45 (modified by , 14 years ago) (diff) |
|---|
GAIIA
- The team: Mihai Istin - mihai.istin , Andreea Visan - andreea.visan
Abstract
Task scheduling is one of the most important management aspects in a distributed system because this component should achieve two main goals: on the one hand efficient use of available resources and on the other hand high performance in solving tasks. Because of the fact that the scheduling problem is an NP-Complete problem, a near-optimal algorithm is a desired solution. A third goal is the fact that the algorithm should provide the results very fast. This project's aim is to develop a parallel solution for a near-optimal algorithm for dependent task scheduling in distributed systems.
Technologies and Languages
- C/C++
- MPI
- OPENMP
Project Activity (main steps)
- the serial solution - OPENMP tunning - MPI tunning - experimental tests, conclusions
Details
The Problem
The input:
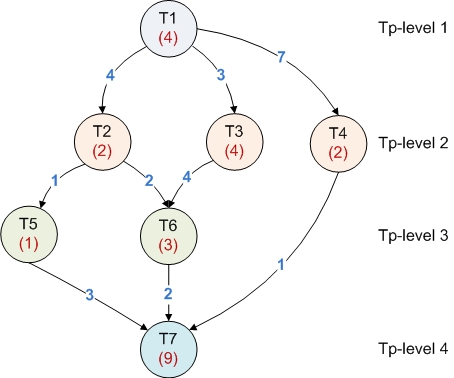
- The graph of tasks that have to be scheduled. Each task is represented as a node while the dependencies between tasks are represented as edges. Each tasks (node) has associated a computational cost and each dependency (edge) has an communication costs.
- The processor topology graph which is also described as a DAG. Each node represent a processor (and the weight represents the speed) while each edge represents the communication cost between processors.
The output:
- The schedule with contains the mapping of tasks on processors and the order of tasks to be executed on the same processor.
The goal:
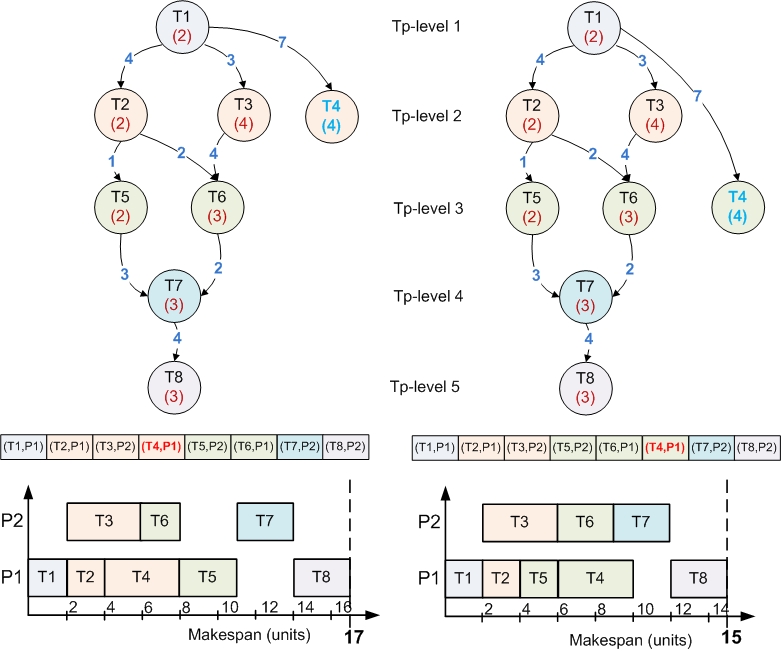
- load balancing
- minimum makespan
- minimum idle times
The proposed algorithm
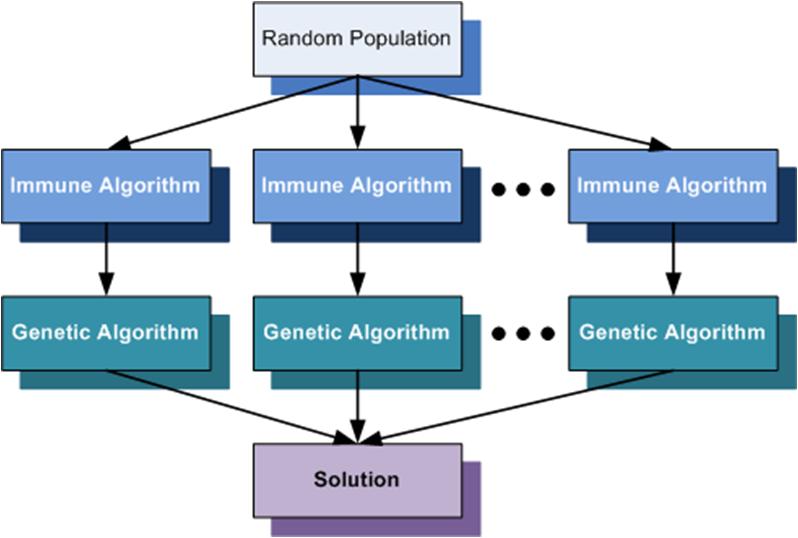
Our solution is based on a hybrid evolutionary algorithm with combines the benefits of genetic and immune algorithms algorithms in order to provide efficient solutions. It is known that the convergence time of genetic algorithms is highly influenced by the average fitness of the initial population. So if we could find a way to provide a population with an good average fitness at the initialization phase of the genetic algorithm, the algorithm will converge faster.
Immune algorithms are also bio-inspired algorithms that are based on the human immune system model. They evolve a population of antibodies in order to fit better the antigens that are threatening the immune system.
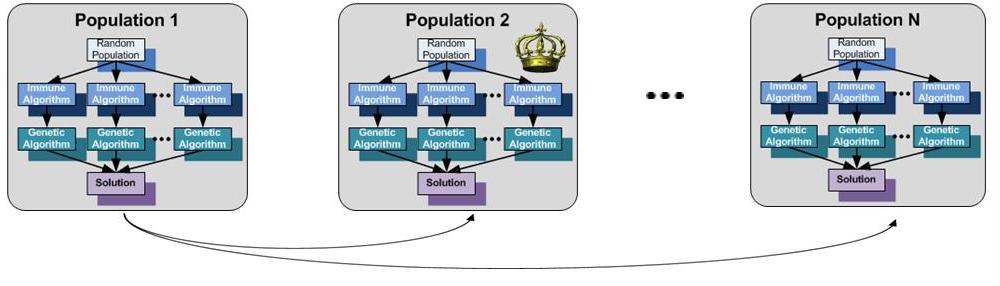
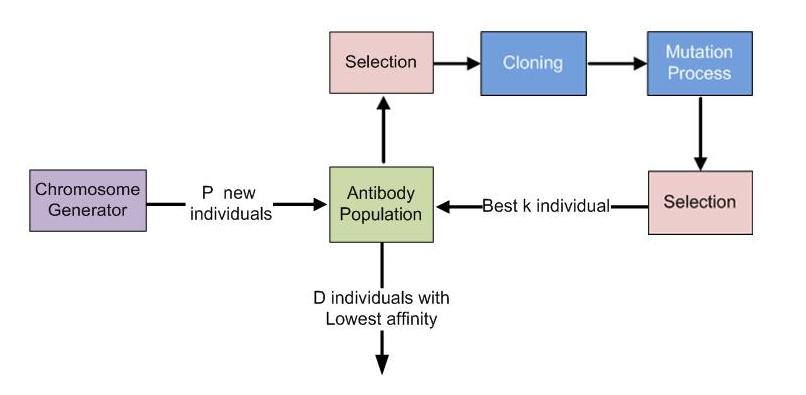
As a computational model, immune algorithms can be designed to evolve a population of chromosomes representing the antibodies in order to have a good fitness. The implementation of such algorithms is based on the clonal selection principle which model the response of an immune system to an intruder. Basically, the current population of antibodies is evaluated and the best individuals (individuals with the best fitness) are selected for the maturation process. During this process, for each selected individual will be made a number of clones proportionally with its fitness. Then each clone will suffer multiple mutations. The number of mutations will be inverse proportionally with its fitness. Then, the clones are evaluated, and the best are selected in order to survive to the next generation. The antibodies with the lowest fitness will be removed from the current population.
The main advantage of immune algorithms is that they are capable of evolving a population with a good average fitness after only several iteration. On the other hand these algorithms have also a drawback: as a consequence of the fact that the mutation rate varies inverse proportionally with the fitness, the best individuals will be similar. But if we are aware of this drawback we can control the diversity of the evolved population by using only a few generations and by using reinsertion.
The genetic algorithm
1. Chromosome representation
The chromosome representation is based on the topological levels of the nodes. The order of the nodes within a chromosome is a valid topological sort where the first node is an entry node (it has no successors) while the last node is an exit node (it has no successor).
This chromosome encoding assures that none of the genetic operators that will be further described will not violate the dependencies between tasks. So this seems to be a very convenient encoding, but it also has drawbacks which consist in the fact that the explorable solution space will not be entirely covered. This happens because there are some special nodes that can be placed on multiple topological levels without violating the topological order. These nodes are called floating nodes and are characterized as nodes that have a maximum topological level grater than their minimum topological level. The minimum topological level is the level computed during an usual topological sort, while the maximum topological level is the one computed on the transposed graph.
Genetic operators
- Single Point Crossover
The crossover operator for a chromosome representation used follows the following steps:
- a cut position is randomly selected ( in the above example the cut point is chosen between genes four and five) and for each chromosome results a head and a tail segment;
- the first offspring is obtained by joining the head segment of the first parent with the combination of the tail segments both parents; more specific, for each gene the task is taken from the first parent and the assigned task is taken from the parent;
- the second offspring is obtain the same way, using the head segment of the first parent and the combination of tail segments of both parents, but this time, the tasks are taken from the second parent while the assigned processors are taken from the first parent
b Simple Gene Mutation
First is selected a chromosome and a randomly selected gene is changed by assigning the task described by the gene to a new processor with the earliest start time.
- Swap Gene Mutation
It is selected a processor that is assigned to run at least two jobs with topological level. Then are randomly selected two tasks with the same topological level assigned to the current processor and the tasks are interchanged if the first task to execute has less children then the second one
- Topological Hyper-Mutation
Whenever a chromosome is affected by this type of mutation, a node from the free node list is randomly selected. Its current topological level is increased and its position in the chromosome is modified in order to reveal the new topological order. Then, all direct predecessors of the selected node are investigated to decide whether they became free floating nodes. If they do, they are inserted in free floating node list corresponding to the current chromosome. If the modified node is no longer a free floating node list (its topological level is equal to the minimum topological level of its successors minus 1), it is removed from the list.
The Immune Algorithms
In the following figure is presented the general model for the immune algorithms.
The number of clones is computed using the following formula
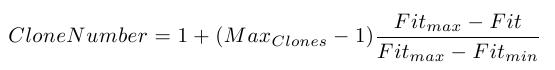
while for the number of mutations we use
The Parallel Solution
- The Parallel Execution Model
- The Distributed Execution Model
Compiling, Running, Profiling
- the OpenMP version
g++ -g -fopenmp -o scheduler main.cpp ...
qsub -q ibm-quad.q -pe openmpi 1 -v OMP_NUM_THREADS=4 script.h
Experimental results
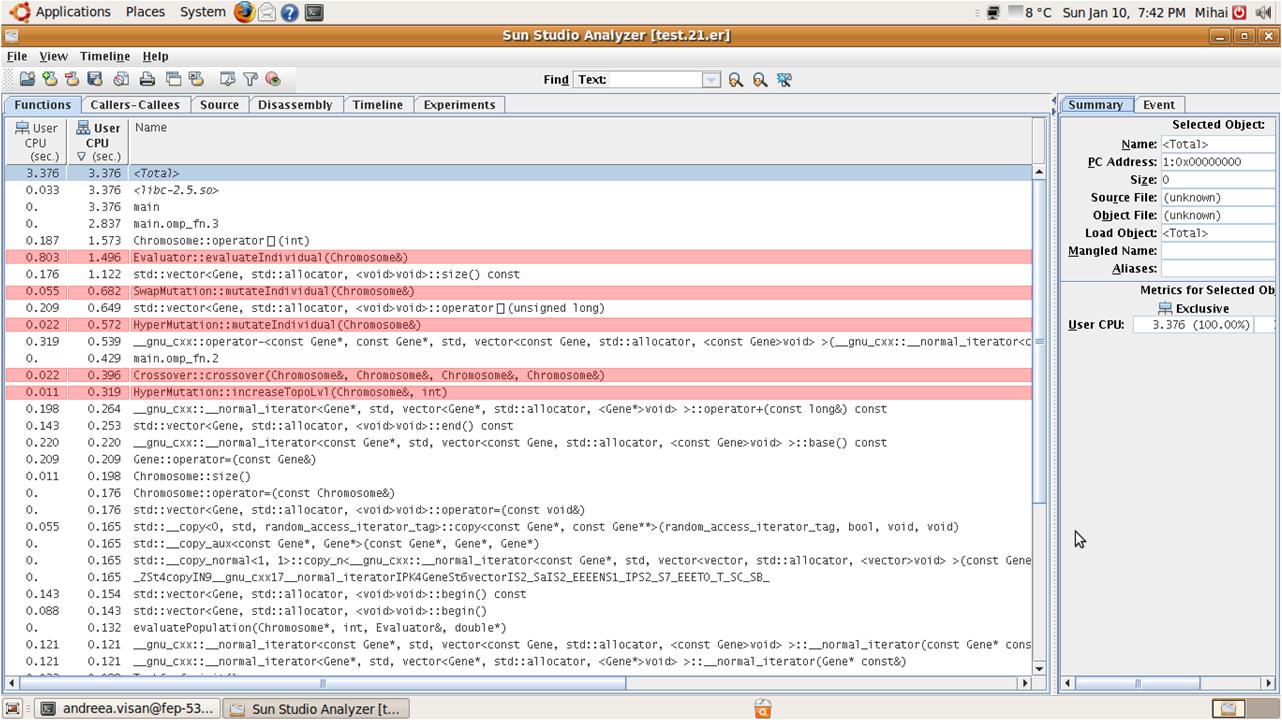
Sun Studio Performance Analyzer results:
- function overview
- OMP version - 1 thread
- OMP version - 2 thread
- OMP version - 4 thread
- OMP version - 8 thread
- Evolution - Summary
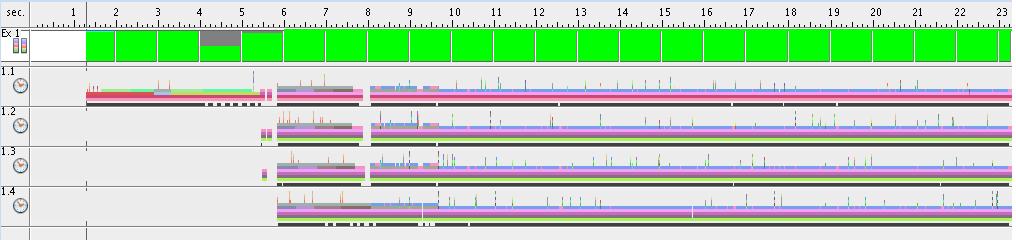
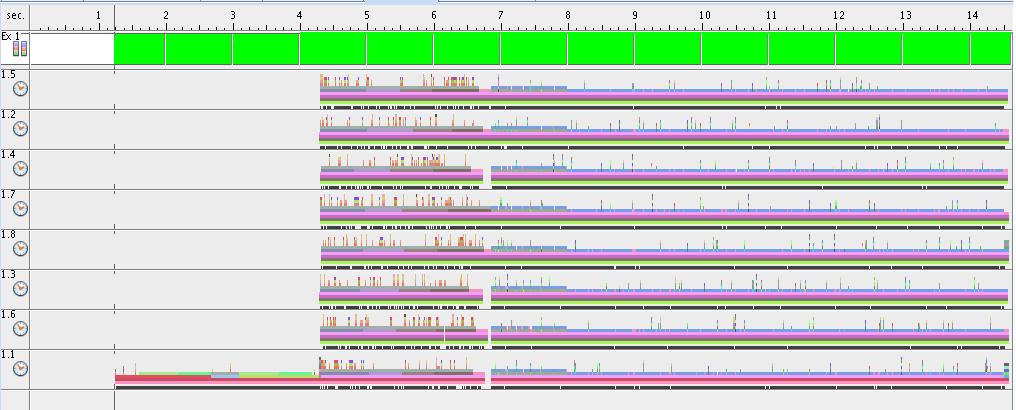
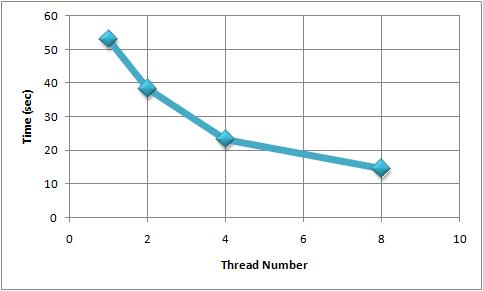
- Execution time for each thread (8 threads situation)
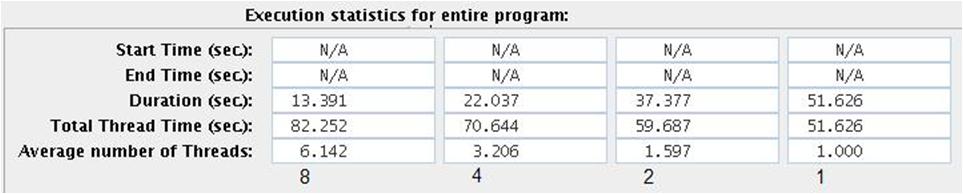
- Execution statistics for the entire program for 1,2,4 and 8 threads
Attachments (23)
-
chromosome.jpg (18.2 KB) - added by 14 years ago.
The chromosome's representation
-
DAG.jpg (52.1 KB) - added by 14 years ago.
The DAG of tasks
-
floating_nodes.jpg (170.8 KB) - added by 14 years ago.
Example of floating nodes
- 1.jpg (29.2 KB) - added by 14 years ago.
-
2.jpg (37.1 KB) - added by 14 years ago.
Execution - 2 threads
-
4.jpg (50.1 KB) - added by 14 years ago.
Execution - 4 threads
-
8.jpg (76.4 KB) - added by 14 years ago.
Execution - 8 threads
-
overview.jpg (124.1 KB) - added by 14 years ago.
Sun Studio Performance Analyzer - function overview
-
ia.jpg (22.6 KB) - added by 14 years ago.
The Immune Algorithm
-
execp.jpg (37.0 KB) - added by 14 years ago.
(Parallel) Execution model
-
execd.jpg (41.3 KB) - added by 14 years ago.
(Distributed) Execution model
- grafic2.jpg (170.1 KB) - added by 14 years ago.
-
grafic1.jpg (16.6 KB) - added by 14 years ago.
Evolution (thread)
- runtime.jpg (21.1 KB) - added by 14 years ago.
- tab.jpg (13.1 KB) - added by 14 years ago.
- tab2.jpg (29.3 KB) - added by 14 years ago.
- form1.jpg (5.8 KB) - added by 14 years ago.
- form2.jpg (6.4 KB) - added by 14 years ago.
- form3.jpg (9.6 KB) - added by 14 years ago.
- tour.jpg (19.7 KB) - added by 14 years ago.
- sort1.jpg (21.4 KB) - added by 14 years ago.
- sort2.jpg (16.6 KB) - added by 14 years ago.
- multi.png (25.4 KB) - added by 14 years ago.
Download all attachments as: .zip
![(please configure the [header_logo] section in trac.ini)](/trac/PP2009/chrome/site/your_project_logo.png)