Logic programming

By using nonlinear operators, logic programming is easily added to YALMIP. The logic programming module is not intended to be used for large logic programs, but is only implemented to help the user to add a small number of logic constraints to a standard model. Note that logic constraints leads to a problem with binary variables, hence mixed integer programming is needed to solve the problem. The logic functionality has not been tested much, and was mainly implemented to show the strength of nonlinear operators. A lot of features are still lacking, but are typically easy to add. If you need it, make a feature request!

Simple logic constraints

As a first example, let us solve a simple satisfiability problem. Note the use of binary variables and the TRUE operator (the true operator takes a variable x and returns the constraint x≥1.)

binvar a b c d e f
F = set(true((a & b & c) | (d & e & f)));
solvesdp(F);
double([a b c d e f])
ans =
     0     0     0     1     1     1

A constraint with a scalar logic expression, generated by the operators AND or OR, is automatically handled as a truth constrained variable (although it is strongly advised to use the truth operator.) Hence the following constraint is equivalent.

F = set((a & b & c) | (d & e & f));
solvesdp(F);
double([a b c d e f])
ans =
     0     0     0     1     1     1

A truth constraint on a standard variable must however be explicitly stated

F = set((a & b & c) | (d & e & f)) + set(true(d));
solvesdp(F);
double([a b c d e f])
ans =
     0     0     0     1     1     1

or equivalently

F = set((a & b & c) | (d & e & f)) + set(d >= 1);
solvesdp(F);
double([a b c d e f])
ans =
     0     0     0     1     1     1

To constrain an expression to be false, use the FALSE operator,

F = set(false((a & b & c) | (d & e & f)));
solvesdp(F);
double([a b c d e f])
ans =
     1     0     0     1     0     0

or simply add the corresponding numerical constraint (Notice that we use inequality instead of equality constraint. The reason is rather technical but it is recommended, since the convexity propagation algorithm used for expanding the nonlinear operators might fail otherwise)

F = set(((a & b & c) | (d & e & f)) <= 0);
solvesdp(F);
double([a b c d e f])
ans =
     1     0     0     1     0     0

Objective functions are allowed.

F = set(((a & b & c) | (d & e & f)) <= 0);
solvesdp(F,-a-b-c-d-e-f);
double([a b c d e f])
ans =
     1     0     1    1     0     1

In addition to the operators AND (&), OR (|) and NOT (~), the operator IMPLIES(X,Y) is implemeted. To force e to be true if f is true, we use IMPLIES.

F = set(((a & b & c) | (d & e & f)) <= 0) + set(implies(f,e));
solvesdp(F,-a-b-c-d-e-f);
double([a b c d e f])

An equivalent formulation is

F = set(((a & b & c) | (d & e & f)) <= 0) + set(e >= f);
solvesdp(F,-a-b-c-d-e-f);
double([a b c d e f])

Mixed logic and conic constraints

The first construction for creating mixed constraints is IMPLIES. The following trivial program ensures the symmetric matrix X to have eigenvalues larger than 1 if a or b is true. The result is a mixed integer semidefinite problem which will be solved using YALMIPs mixed integer solver. Be warned, a lot of the functionality here is experimental. Please validate your results and report any oddities as usual.

binvar a b
X = sdpvar(3,3);
F = set(implies(a | b, X > eye(3)));
solvesdp(F)

The following construction ensures the variable x to be contained in a polytope if d is true

A = randn(5,2);
b = rand(5,1);
x = sdpvar(2,1);
d = binvar(1,1);
F = set(implies(d,A*x <=b))

A related command is if-and-only-if, IFF, i.e. logic equivalence. The following code force the variable x to be contained in a polytope if y is contained in the polytope, and vice versa.

A = randn(5,2);
b = rand(5,1);
x = sdpvar(2,1);
y = sdpvar(2,1);
F = set(iff(A*x <= b, A*y <= b))

This functionality can be used to model various logic constraints. Consider for instance the constraint that a variable is in one of several polytopes.

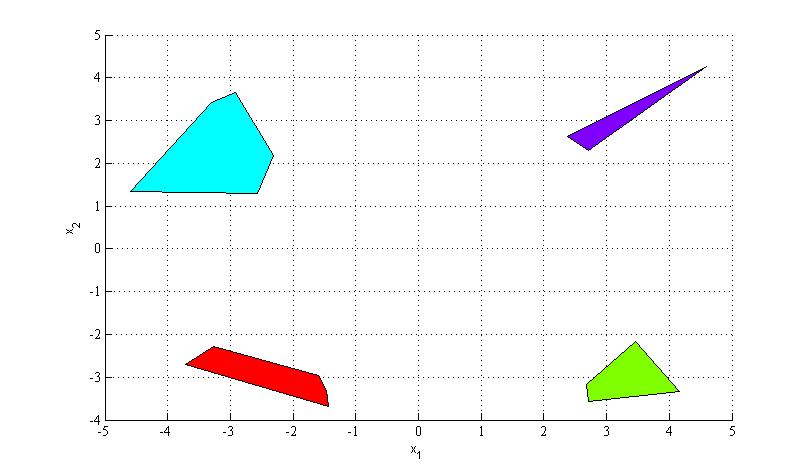
The data and plot was generated with the following code (assuming MPT is installed)

A1 = randn(8,2);
b1 = rand(8,1)*2-A1*[3;3];
A2 = randn(8,2);
b2 = rand(8,1)*2-A2*[-3;3];
A3 = randn(8,2);
b3 = rand(8,1)*2-A3*[3;-3];
A4 = randn(8,2);
b4 = rand(8,1)*2-A4*[-3;-3];
plot(polytope(A1,b1),polytope(A2,b2),polytope(A3,b3),polytope(A4,b4))

We will now try to find a point x as far up in the figure as possible, but still in one of the polytope. First, we define 4 binary variables, each one describing whether we are in the corresponding polytope, and add the constraint that we are in at least one polytope.

binvar inp1 inp2 inp3 inp4
F = set(inp1 | inp2 | inp3 | inp4);

To connect the binary variables with the polytopes, we use the IFF operator.

x = sdpvar(2,1);
F = F + set(iff(inp1,A1*x < b1));
F = F + set(iff(inp2,A2*x < b2));
F = F + set(iff(inp3,A3*x < b3));
F = F + set(iff(inp4,A4*x < b4));

Finally, we solve the problem by maximizing the second coordinate of x.

solvesdp(F,-x(2));

double(x)
ans =
    4.5949
    4.2701
double([inp1 inp2 inp3 inp4])
ans =
     0     0     0     1

The IFF is overloaded as equality, hence the following code generates the same problem.

F = set(inp1 | inp2 | inp3 | inp4);
F = F + set(inp1 == (A1*x < b1));
F = F + set(inp2 == (A2*x < b2));
F = F + set(inp3 == (A3*x < b3));
F = F + set(inp4 == (A4*x < b4));
solvesdp(F,-x(2));

We should mention that it is not necessary to use the IFF operator in this problem, the IMPLIES operator suffice. The implies operator should be used when possible, since it for most cases is more efficiently implemented (less number of additional binary variables) than the IFF function. As a general comment, if you want to play it safe, stay away from IFF as much as possible, and don't use IMPLIES with the first argument being anything else than a binary variable. 

F = set(inp1 | inp2 | inp3 | inp4);
F = F + set(implies(inp1,A1*x < b1));
F = F + set(implies(inp2,A2*x < b2));
F = F + set(implies(inp3,A3*x < b3));
F = F + set(implies(inp4,A4*x < b4));
solvesdp(F,-x(2));

double(x)
ans =
    4.5949
    4.2701

The IFF operator is used internally to construct mixed constraints involving OR. With this functionality, we can solve the previous problem using a more intuitive code (albeit possibly inefficient since it will use IFF instead of IMPLIES).

F = set( (A1*x < b1) | (A2*x < b2) | (A3*x < b3) | (A4*x < b4));
solvesdp(F,-x(2));

double(x)
ans =
    4.5949
    4.2701

Improving the Big-M formulation

The conversion from logic constraints to mixed integer constraints is done in YALMIP using a standard big-M formulation. By default, YALMIP uses a big-M value of 104, but it is recommended to add constraints to improve this. By explicitly adding bounds on variables, YALMIP can exploit these bounds to compute a reasonably small big-M constant.

x = sdpvar(2,1);
F = set( (A1*x < b1) | (A2*x < b2) | (A3*x < b3) | (A4*x < b4));
F = F + set(-100 < x < 100);
solvesdp(F,-x(2));

double(x)
ans =
    4.5949
    4.2701

Adding bounds can significantly improve the strength of the relaxations and corresponding reduction of computation time. Hence, if you know, or can estimate, lower and upper bounds, let YALMIP know this. If you fail to add bounds, YALMIP will issue warnings.

Sudoku example

There are not many logic constructions implemented at the moment, but they can easily be added if you make a request. As an example, the logic constraint ALLDIFFERENT was easily implemented as a nonlinear operator. Let us use the operator to solve a Sudoku game.

S = [0,0,1,9,0,0,0,0,8;6,0,0,0,8,5,0,3,0;0,0,7,0,6,0,1,0,0;...
     0,3,4,0,9,0,0,0,0;0,0,0,5,0,4,0,0,0;0,0,0,0,1,0,4,2,0;...
     0,0,5,0,7,0,9,0,0;0,1,0,8,4,0,0,0,7;7,0,0,0,0,9,2,0,0];
ans =
0  0  1  9  0  0  0  0  8
6  0  0  0  8  5  0  3  0
0  0  7  0  6  0  1  0  0
0  3  4  0  9  0  0  0  0
0  0  0  5  0  4  0  0  0
0  0  0  0  1  0  4  2  0
0  0  5  0  7  0  9  0  0
0  1  0  8  4  0  0  0  7
7  0  0  0  0  9  2  0  0

In case you have missed out on the Sudoko hype, the goal is to replace the zeros with numbers between 1 to 9, keeping elements in all rows and columns different, and keeping all elements in the 9 3x3 blocks different.

Let us create our 9x9 integer decision variable and define the basic constraints

M = intvar(9,9,'full');

fixed = find(S);
F = set(1 <= M <= 9) + set(M(fixed) == S(fixed));

We add the logic constraints using some MATLAB indexing tricks, add some redundant cuts, and solve the problem (The solution time depends highly on your MILP solver. CPLEX solves this problem in roughly 0.1 seconds, while GLPK fails.)

for i = 1:3
    for j = 1:3
        block = M(find(kron(full(sparse(i,j,1,3,3)),ones(3))));
        F = F + set(alldifferent(block));
    end
end

for i = 1:9
    F = F + set(alldifferent(M(i,:)));
    F = F + set(alldifferent(M(:,i)));
end

F = F + set(sum(M,1) == 45) + set(sum(M,2) == 45);
solvesdp(F);

Note that this model of the Sudoku game is pretty weak. A much better model can be obtained by using a scheme based on having a binary for each possible value for each element. This is left as an exercise.

Variable index variables

By combining the framework for nonlinear operators and logic programming, YALMIP allows variable indices. The following silly example picks out the two highest indices of elements in a vector p smaller than or equal to three.

sdpvar i j
x = sdpvar(1,8);
p = [0 1 7 2 3 4 3 20];
solvesdp(set(x == p)+set(x([i j]) <= 3)+set(i~=j),-i-j);
double([i j])
ans =
     5     7

Behind the scenes

The logic AND and OR operators are implemented using nonlinear operators. As an example, to implement the OR operator z=or(x,y) for binary x and y, the simple code below is sufficient (the code actually used is slightly different to improve performance for expressions with more than two variables, but the idea is the same). The first constraint ensures that z is false if both x and y are false, the two following constraints ensure that z is true if x or y is true, while the last constraint constrains z to be a binary (true/false) variable.

function varargout = or(varargin)
% SDPVAR/OR

switch class(varargin{1})
    case 'char'
        z = varargin{2};
        x = varargin{3};
        y = varargin{4};
        
        varargout{1} = set(x + y >= z) + set(z >= x) + set(z >= y) + set(binary(z));
        varargout{2} = struct('convexity','milp','monotonicity','milp','definiteness','milp');
        varargout{3} = [x y];
    case 'sdpvar'
        x = varargin{1};
        y = varargin{2};
        varargout{1} = yalmip('addextendedvariable','or',varargin{:});
    otherwise
end

The operators IFF and IMPLIES are just standard implementations of big-M reformulations, implemented in the nonlinear operators framework.