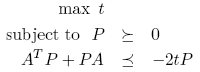Decay-rate estimation

The problem we will solve is to estimate the decay-rate of a linear system x' = Ax. This can be formulated as a generalized eigenvalue problem.

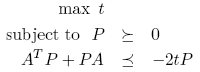
Due to the product between t and P, the problem cannot be solved directly. However, it is easily solved by bisection in t.

Define the variables.

A = [-1 2;-3 -4];
P = sdpvar(2,2);

To find a lower bound on t, we solve a standard Lyapunov stability problem.

F = set(P>eye(2))+set(A'*P+P*A < -eye(2));
solvesdp(F,trace(P));
P0 = double(P);

In the code above, we minimized the trace just to get a numerically sound solution. This solution gives us a lower bound on decay-rate

t_lower = -max(eig(inv(P0)*(A'*P0+P0*A)))/2;

We now find an upper bound on the decay-rate by doubling t until the problem is infeasible. To find out if the problem is infeasible, we check the field problem in the solution structure. The meaning of this variable is explained in the help text for the command yalmiperror. Infeasibility has been detected by the solver if the value is 1. To reduce the amount of information written on the screen, we run the solver in a completely silent mode. This can be accomplished by using the verbose and warning options in sdpsettings.

t_upper = t_lower*2;
F = set(P>eye(2))+set(A'*P+P*A < -2*t_upper*P);
ops = sdpsettings('verbose',0,'warning',0);
sol = solvesdp(F,[],ops);

while ~(sol.problem==1)
    t_upper = t_upper*2;
    F = set(P>eye(2))+set(A'*P+P*A < -2*t_upper*P);
    sol = solvesdp(F,[],ops);
end

Having both an upper bound and a lower bound allows us to perform a bisection.

tol = 0.01;
t_works = t_lower
while (t_upper-t_lower)>tol
  t_test = (t_upper+t_lower)/2;
  disp([t_lower t_upper t_test])
  F = set(P>eye(2))+set(A'*P+P*A < -2*t_test*P);
  sol = solvesdp(F,[],ops);
  if sol.problem==1
    t_upper = t_test;
  else
    t_lower = t_test;
    t_works = t_test;
 end
end

This example will be revisited later when we study BMIs